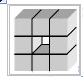
Eight cubes are glued together to form the figure shown. The length of an edge of each cube is 3 cm. The entire figure is covered in paint. How many square centimeters are covered in paint?
|
METHOD 1: Strategy: Temporarily disregard the first 1/5 mile.
Dan pays $2.00 for the first fifth mile and $7.60 for the rest of the ride. Each fifth of a mile costs 40¢, and 760 ÷ 40 = 19. The $7.60 pays for a ride of 19 fifths of a mile. Adding 1/5 mile for the first $2.00, the longest ride Dan can afford is 20/5 or 4 miles. METHOD 2: Strategy: Make a table. The cost increases by $.40 for each fifth of a mile. When the desired amount is reached, the taxi will have traveled a length of 20/5 or 4 miles. METHOD 3: Strategy: Use algebra. Let N = the number of fifths of a mile after the first fifth mile that Dan can ride. 2.00 + .40N = 9.60 .40N = 7.60 (Subtract 2.00 from each side) N = 19 (Divide each side by .40) Add the first fifth of a mile, bringing the length of the ride to 20/5 or 4 miles. Remember, you can begin posting this Friday, January 13th :) But no later than January 28th!!
A taxi ride costs $2 for the first 1/5 mile and 40 cents for each additional 1/5 mile. Dan has $9.60. What is the longest taxi ride he can afford, in miles?(Express your answer in simplest form.) The Answer is: 7
METHOD 1: Strategy: Use the definition of a week. In 45 consecutive days there are 6 weeks and 3 days. Each of the 6 weeks contains one Monday. In order to have the greatest number of Mondays, one of the 3 days left must also be a Monday. The greatest number of Mondays that can occur in 45 consecutive days is 7. METHOD 2: Strategy: Start at 1 and count by sevens. Suppose day 1 is a Monday. Mondays will occur on days 1, 8, 15, 22, 29, 36, 43. The next Monday would be after day 45. The greatest number of Mondays in 45 consecutive days is 7. What is the greatest number of Mondays that can occur in 45 consecutive days?
Answer is: 49 and 77
METHOD 1: Strategy: Examine the possible prime factors of N. N is composite, so it is the product of two or more (not necessarily different) primes. None of the prime factors can be 2, 3, or 5, for then at least one of the fractions given would not be in lowest terms. The possible prime factors of N are 7, 11, 13, 17, etc. The composites using these factors are 7 × 7, 7 × 11, 7 × 13, 11 × 11, etc. Because only the first two composites are between 20 and 80, the only possible values of N are 49 and 77. METHOD 2: Strategy: Determine the whole numbers between 20 and 80 that don't work. Start with the numbers 21, 22, 23, . . ., 79. 2/N , 3/N , and 5/N are in lowest terms, so eliminate multiples of 2, 3, and 5. This leaves 23, 29, 31, 37, 41, 43, 47, 49, 53, 59, 61, 67, 71, 73, 77, and 79. N is composite, so eliminate primes, leaving only 49 and 77 The possible values of N are 49 and 77. Answer is 11
METHOD 1: Strategy: Find the sum of the five numbers. If the average of the five numbers is 8, then the sum of those five numbers is 5 × 8, or 40. Subtract the sum of the two known numbers, 7, from 40. The sum of the other three numbers is 33. The value of any one of the three equal numbers is 33 ÷ 3, or 11. METHOD 2: Strategy: Start with all equal. The simplest set of 5 numbers whose average is 8 is 8, 8, 8, 8, and 8. Replacing one of the 8's with 2 drops the total by 6, and replacing another with 5 drops the total still further by 3. The total of the five numbers must be increased by 9 (since 6 + 3 = 9), so each of the three remaining 8's must be increased by 3 (three 3's = 9). That means the numbers are 2, 5, and three 11's. The value of any one of the three equal numbers is 11. FOLLOW-UPS: The average of five different natural numbers is 8. Consider the largest of these numbers.(1)What is its largest possible value? [30] (2) What is its smallest possible value? [10] |
AuthorWe are peers working as a collaborative group. Archives
March 2012
Categories |


 RSS Feed
RSS Feed
